Branching Shadows

Problem Statement

The problem of creating realistic images of trees and plants lies beyond simply creating the correct geometry and correct textures—rendering this data realistically and with real-world detail poses a unique problem. How does one ray-trace a realistic forest scene? The sheer amount of data alone would soon overwhelm both memory resources and computing time. This project will attempt to formulate and implement a practical method for ray-tracing trees and plants that avoids or reduces these exorbitant costs.

Background

There is an enormous amount of research done on generating tree and plant geometry through the use of L-systems. [2, 3, 4] The 'L' comes from the last name of Aristid Lindenmeyer, who first introduced the idea. (See Summary Of L-Systems). When it comes to the visualization of L-systems, it seems that the usual computer graphics trend of dividing geometry and rendering has prevailed—the L-system creates the geometry and hands it off to the renderer. Most of what I've read on the subject comes from The Algorithmic Beauty Of Plants [4] and some of the papers listed at [2]. Much of the time there is simply no mention of the rendering process and I simply assumed that no special rendering method was used (either standard ray-tracing or Z-buffer style algorithms). The closest I could find to a unique rendering method was the notion of "voxel automata" by Greene [5]. But for a large number of trees, the storage space for the voxels seems prohibative.

There was, however, research done in Synthetic Topiary [3] which relates to the method I hope to use for limiting tree branches inside bounding shapes. The idea there was to create "environmentally sensitive" L-systems which could alter the plant's growth based on either obstacles or internally defined boundaries.

Summary of L-Systems

Quoted from [3], here is a brief overview of L-systems:

An L-system is a parallel rewriting system operating on branching structures represented as bracketed strings of modules. Matching pairs of square brackets enclose branches. Simulation begins with an initial string called the axiom, and proceeds in a sequence of discrete derivation steps. In each step, rewriting rules or productions replace all modules in the predecessor string by successor modules. The applicability of a production depends on a predecessor's context (in context-sensitive L-systems), values of parameters (in productions guarded by conditions), and on random factors (in stochastic L-systems). In the most extensive case, a production has the format:

id : lc < pred > rc : cond —> succ : prob

where id is the production identifier (label), lc, pred, and rc are the left context, the strict predecessor, and the right context, cond is the condition, succ is the successor, and prob is the probability of production application. The strict predecessor and the successor are the only mandatory fields. For example, the L-system given below consists of axiom w and three non-identity productions p1 , p2 , and p3 .

w : A(1)B(3)A(5)
p1 : A(x) —> A(x + 1) : 0.4
p2 : A(x) —> B(x - 1) : 0.6
p3 : A(x) < B(y) > A(z) : y < 4 —> B(x + z)[A(y)]

The stochastic productions p1 and p2 replace module A(x) either by A(x+1) or by B(x-1), with probabilities equal to 0.4 and 0.6, respectively. The context-sensitive production p3 replaces a module B(y) with left context A(x) and right context A(z) by module B(x+z) supporting branch A(y). The application of this production is guarded by condition y < 4. Consequently, the first derivation step may have the form:

A(1)B(3)A(5) ==> A(2)B(6)[A(3)]B(4)

It was assumed that, as a result of random choice, production p1 was applied to the module A(1), and production p2 to the module A(5). Production p3 was applied to the module B(3), because it occurred with the required left and right context, and the condition 3 < 4 was true.

In contrast to the parallel application of productions in each derivation step, the interpretation of the resulting strings proceeds sequentially, with the reserved modules acting as commands to a LOGO-style turtle [27, 28, 29]. At any time, the turtle is characterized by a position vector P and three mutually perpendicular orientation vectors H, U , and L, indicating the turtle's heading, the up direction, and the direction to the left. Module F causes the turtle to draw a line in the current direction. Modules +, -, &, ^, /, and \ rotate the turtle around one of the vectors H, U, or L. The length of the line and the magnitude of the rotation angle can be given globally or specified as parameters of individual modules. During the interpretation of branches, the opening square bracket pushes the current position and orientation of the turtle on a stack, and the closing bracket restores the turtle to the position and orientation popped from the stack. A two-symbol module @o draws a sphere at the current position. A special interpretation is reserved for the module %, which cuts a branch by erasing all symbols in the string from the point of its occurrence to the end of the branch.
 

Approach and Methodology

My first thoughts on how I'd go about this can be illustrated with the following:
 

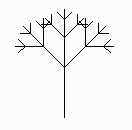Simple tree-like structure.

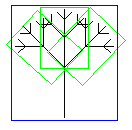Bounding shape around entire tree and first level branches.

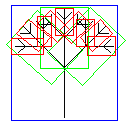Bounding shapes on next level of branches. Etc.

Where the bounding shapes could be either cubes or cylinders. In truth, there is nothing hard about doing this—given the rules that generated the tree, it would be easy to come up with bounding shapes for each branch. An intersecting ray could test the first-level bounding shape and if hit, test the axial tree (non-branching, central structure) and the second-level bounding shapes. If any of these bounding shapes are hit, further intersection depth could be traversed until no bounding shapes remain. One could possibly expect complexity around O(log N), where N is the total number of branches and the base of the logarithm would be the average number of branches on each limb.

But as stated in the Problem Statement, there is the difficulty with the enormous amount of data generated for a single tree. Adding bounding boxes to each branching level only compounds this problem. For that reason, I wish to approach the problem with the notion of generating both data and bounding shapes at render-time. In the most extreme case, all that would be stored is the outer bounding shape and the "seed" data necessary to generated the tree. A. R. Smith coined the phrase "data amplification" [6] to describe the process of amplifying a small amount of data into a large amount. By adding length to the render-time, this "data amplification"—with L-systems, the process of iterating the grammar productions—could occur every time a ray intersects the outer bounding shape. The question to answer is where and to what extent this "data amplification" occurs.

Possibly the most difficult aspect of this problem is incorporating bounding shapes, render-time geometry creation, and L-systems into one consistent model. At first I could not think of a way to incorporate bounding shapes into L-systems and thought instead of creating an alternative to L-systems—one that would use bounding shape generation as an inherent component of the geometry generation. Later, I had the idea of associating a "relative" bounding shape with each branch occuring in any given L-system production. By "relative", I mean that it would be relative to the parent bounding shape in dimension. With this method, the entire L-system could be generated before rendering and the maximum relative bounding shape could be computed for each branch in the L-system (specified by [...]). In the course of the project, it could be discovered that using L-systems—although theoretically elegant—might be too computationally intensive to be generated for every ray, in which case my original, alternative solution might be more feasible.

To solve all of these problems, I would probably start simple and expand with the following steps:

1. Build a simple, possibly parametric, L-parser and then generate some simple wire-frame images using cubes or cylinders for each limb.
2. Extend my ray-tracer from last quarter to ray-trace cylinders and/or cubes and use the output from the L-parser to create my first images using simple linear intersection testing.
3. Possibly experiment with generating the geometry at render-time but still use the linear method.
4. Extend the L-parser to calculate relative bounding shapes for each branch.
5. Extend the ray-tracing method to use the bounding shapes. This would involve letting the user specify how much detail to generate before render-time and how much to generate during render time. This would also involve specifying how "deep" the bounding shapes are generated—at some point the bounding shape overhead would override any benefits.
6. Create a BSP or octree version to compare performance.
7. Write a paper summarizing all results and performance comparisons.
8. Create some cool images.
9. Do optional extensions (see Goals).

 Goals

The central goals for this project are the following:

• Define and implement a feasible way to incorporate bounding shapes into traditional L-systems. If it is found that this method is faulty or applicable to only a subset of L-systems, then these limitations would be defined and possible alternatives proposed.
• Explore the possibilities of render-time "data amplification" using the bounding shape L-system method.
• Compare the performance of the bounding-shape method along with run-time geometry generation with traditional methods such as linear and either octree or bsp trees.
• Create some really cool pictures that might have been difficult to generate with previous methods. These would be generated using my ray-tracer built from last quarter.

Secondary (optional) goals which could be achieved given enough time include:

• An interactive user interface for creating L-systems. This would include not only wire frame viewing of L-systems but also graphical ways to create L-system productions.
• Implant the tree-tracing method into a "real" ray-tracer such as the POV (Persistence Of Vision) Ray Tracer. (Source distributed freely).
• Expand the L-parser to be context-sensitive, stochastic, and fully parametric (symbolic, not just numeric, parameters).
• Implement "environmentally sensitive" extentions as in [3] and extend that idea to take into account my bounding-shape method.
• Explore all of the possible benefits of placing tree generation into the renderer—i.e. curved sufaces, aliasing, "snow" on the branches, etc.

Time Line and Milestones

The following time-line is based on the steps outline in the Approach and Methodology section.

 

References

1. www.xs4all.nl/~ljlapre/main.htm
2. www.cpsc.ucalgary.ca/projects/bmv/papers/index.html
3. Przemyslaw Prusinkiewicz, Mark James, and Radomir Mech. Synthetic topiary. Proceedings of SIGGRAPH 94 (Orlando, Florida, July 24-29, 1994). In Computer Graphics Proceedings, Annual Conference Series, 1994, ACM SIGGRAPH, pp. 351-358.
4. Przemyslaw Prusinkiewicz, and Aristid Lindenmayer. The Algorithmic Beauty Of Plants. Springer-Verlag, New York, 1990. With James S. Hanan, F. David Fracchia, Deborah R. Fowler, Martin J. M. de Boer, and Lynn Mercer.
5. N. Greene. Voxel space automata: Modeling with stochastic growth processes in voxel space. Proceedings of SIGGRAPH '89 (Boston, Mass. , July 31-August 4, 1989), in Computer Graphics 23,4 (August 1989), pages 175-184, ACM SIGGRAPH, New York, 1989.
6. A. R. Smith. Plants, fractals, and formal languages. Proceedings of SIGGRAPH '84 (Minneapolis, Minnesota, July 22-27, 1984) in Computer Graphics, 18, 3 (July 1984), pages 1-10, ACM SIGGRAPH, New York, 1984.